在上一篇描述的加密方案僅對被動竊聽者具有語義安全性，即在選擇明文攻擊下不可區分（IND-CPA）。許多現實世界的應用需要針對主動攻擊的安全性這一強得多的概念，正式稱為在選擇密文攻擊下不可區分（IND-CCA）。

Fujisaki 和 Okamoto 給出了兩種通用的高效方法 [FO99a, FO99b]，用於將任何 IND-CPA 安全的公鑰加密方案轉換為 IND-CCA 安全的方案。然而，它們的構造和分析依賴於隨機預言啟發法 [BR93]，該啟發法通常並不健全。最近，[Pei14] 描述了針對特定緊湊基於環-LWE 的密碼系統的 Fujisaki-Okamoto 轉換的實例化。

在本小節的其餘部分，描述了兩種相關的範式，用於在標準模型中從格構造主動安全的公鑰加密，即無需隨機預言啟發法。

17.1 從有損陷阱門函數出發
Peikert 和 Waters [PW08] 的工作是第一個從任何類型的格假設，在本例中是 LWE 給出標準模型、IND-CCA 安全密碼系統的工作。他們的構造基於一個他們稱為有損陷阱門函數(lossy trapdoor function) 族的概念，或有損 TDF。在有損 TDF 族中，函數 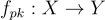的公鑰 pk 可以通過兩種方式之一生成：在單射模式下，pk 與一個陷阱門 sk 一起生成，並且 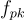是一個可以使用 sk 高效反轉的單射函數。（特別地，值域 Y 必須至少與定義域 X 一樣大。）在有損模式下，pk 在沒有任何陷阱門的情況下生成，並且函數 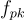是「有損的」，因為它的映像 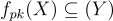比定義域 X 小得多。換句話說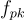， 有許多碰撞，並且典型的 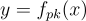，在
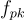下有許多有效的原像。最後，在兩種模式下生成的公鑰是不可區分的：沒有高效對手在區分單射和有損公鑰方面具有顯著優勢。特別是，這最後一個屬性可用於證明反轉單射函數或在有損函數中尋找碰撞都是不可行的。

Peikert 和 Waters 從任何有損 TDF 給出了 IND-CCA 安全加密的通用構造，並且也從 LWE（以及其他假設）構造了一個有損 TDF。他們的加密方案的一個重要屬性是它是見證恢復(witness-recovering) 的：解密演算法設法恢復加密演算法用於創建密文的隨機性，然後重新計算密文以驗證其格式良好。這種技術背離了先前的標準模型 IND-CCA 安全構造，在那些構造中密文本質上攜帶格式良好的零知識證明。[PW08] 的基於 LWE 的有損 TDF 構造在漸近參數和效率上與上面第16篇中描述的被動安全攤銷加密方案大致相同，但具有稍大的常數和對數因子。

17.2 從單射陷阱門函數出發
在 [PW08] 之後不久，Peikert [Pei09] 從 LWE 給出了一個更簡單、更直接的 IND-CCA 安全加密構造。該構造不依賴於任何有損性屬性，但由於使用了 Gentry、Peikert 和 Vaikuntanathan [GPV08] 工作中定義的單射陷阱門函數（如下所述），它仍然是見證恢復的。Peikert 方案的公鑰和密文大小比 [PW08] 中的方案大約大一個線性因子，這主要是由於陷阱門函數的描述更偏向組合（而非代數）。

後來，Micciancio 和 Peikert [MP12] 從 LWE 給出了一個直接的 IND-CCA 安全加密構造，該構造在迄今為止的所有此類構造中具有最佳的漸近和具體參數。該構造緊密遵循了 [Pei09] 基於單射 TDF 的構造，但使用了更緊湊的代數「標記」(tagged) 函數，類似於最初在 [PW08] 中使用的函數。這裡的標記函數是使用 [ABB10] 中的技術獲得的，該技術最初是在基於身份的加密背景下開發的。

17.3 格陷阱門
非正式地，陷阱門函數是一種易於求值但難以自行反轉的函數，但它可以與一些額外的「陷阱門」資訊一起生成，這些資訊使反轉變得容易。這個基本概念有許多版本，取決於所討論的函數是單射、滿射、雙射、「有損」等。典型的候選陷阱門函數是 RSA 函數 [RSA78] 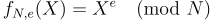，其中 N 是不同質數 p,q 的乘積，且 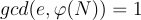。 RSA 函數是 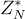上的雙射，陷阱門是 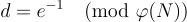。因為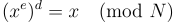
或者，N 的因數分解 p,q 是一個陷門，因為可以從這些因數高效計算 d。相對來說，陷門函數候選較少，在現代密碼學的前幾十年中，所有普遍接受的陷門函數都依賴於假設的整數分解難度 [RSA78, Rab79, Pai99]。

受 Goldreich、Goldwasser 和 Halevi（以下簡稱 GGH）[GGH97] 早期思想的啟發（見第 3.3 節），Gentry、Peikert 和 Vaikuntanathan（以下簡稱 GPV）[GPV08] 表明，某些類型的陷門函數可以從格問題構造，特別是（環-）SIS/LWE。該工作以及幾項後續工作使用這些陷門函數構造了許多強大的密碼學應用，包括數位簽章方案、（分層）基於身份和基於屬性的加密等等。

17.4 陷門功能與實現
在高層次上，格的陷門實現兩種主要的密碼學功能：

• 解決有界距離解碼問題的能力，即找到最接近給定目標點的唯一個格向量，該目標點被保證「相當接近」該格。這可以用來構造單射陷門函數，如 GGH 首次描述。
• 能夠在格的任何所需陪集上，從「相當小」寬度的離散高斯分佈中取樣。這可以用來構造 GPV 所稱的原像可採樣陷門函數（PSF），它產生數位簽章方案和其他應用。非正式地說，PSF 是一個常規的陷門函數 ff，其陷門允許在某一「規範」（但不一定是均勻）分佈下，隨機採樣任何值域元素 y 的原像
  

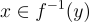
文獻包含兩種不同但密切相關的概念，說明什麼構成了格陷門：

• 第一個概念，用於開創性工作 [GGH97, GPV08, CHKP10] 中，是短基底：本質上，一個由相對較短的格向量組成的格基底。這個概念在概念上非常自然且完全通用，它可以應用於任何格，在下面 17.4.1 會簡單講解一下，用短基底描述高層次直覺和通用演算法。
• 第二個是基於「小工具」(“gadget”-based) 的陷門，在 Micciancio 和 Peikert [MP12] 的工作中引入，並在下面的 17.4.2 中描述。這個概念僅適用於從（環-）SIS/LWE 問題衍生的q-ary格，因此它更專門化。但與短基底相比，小工具陷門在技術上更易於在基於 SIS/LWE 的應用中使用，計算效率更高，並且至少同樣強大。出於這些原因，在後面的章節中，主要用小工具陷門來描述大多數密碼學方案。

17.4.1 短基底
在本部分中，會描述短基底如何作為由「壞」基底（或其他「硬」表示）指定的公共格的陷門，以及這如何產生上述的陷門功能。

重要的鑰的生成:
首先必須考慮如何為同一個格聯合生成一對好基底和壞基底。最初，GGH 建議使用一種臨時方法：隨機選擇一組短的線性獨立向量 S 作為格 L=L(S) 的好基底，然後應用一個「隨機」么模變換 U（具有大條目）來獲得 L 的壞基底 B=S⋅U。或者，Micciancio [Mic01] 建議使用 L 的 Hermite 正規形式基底作為公開的壞基底，該基底在形式意義上是「最難」的基底。

重要的是要注意，上述方法不會從 Ajtai 的 q-ary SIS 格（在第8章中提及) 的最壞情況難解族生成格，因此缺乏證據證明這些方法產生平均難解的問題，而這是安全所需要的。Ajtai [Ajt99] 通過展示如何從 SIS 族生成一個隨機格連同一個相對短的基底來解決這一差距。後續的工作 [AP09, MP12] 簡化並改進了該方法以獲得近乎最優的界。

定理 17.4.1.1 ([Ajt99, AP09, MP12])
存在一個高效的隨機化演算法，給定正整數 n,q 和 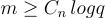（對於某個通用常數 C），輸出一個（近乎）均勻隨機的奇偶校驗矩陣 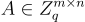指定整數格 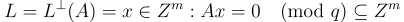連同 L 的一個基底 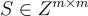，其向量的範數以 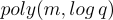為界。

請注意，因為 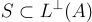，所以會有 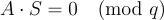。當然，僅當 S 的範數界顯著小於 q（對於典型參數是這種情況）時，該定理才有趣，因為縮放的標準基底向量 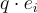。平凡地屬於 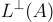。最後，請注意僅僅選擇一個均勻隨機的 A 然後嘗試計算 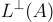中的短向量是不夠的，因為這正是（難解的）SIS 問題。相反，必須以某種方式與 A 一起生成 SS，使得 A 的誘導分佈接近均勻。

來自有界距離解碼的單射陷門函數:
GGH 加密方案的核心是一個單射陷門函數族，其中反轉函數對應於在平均情況下解決有界距離解碼問題。在高層次上，這些函數的工作方式如下：如前所述，公鑰和陷門分別是格 L 的「硬」表示（例如壞基底）和 L 的短基底 S。在隨機輸入上求值函數對應於在對偶格中選擇一個「隨機」向量 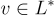和一個短的「誤差」向量 e，其範數顯著小於 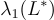，並輸出 t=v+e 使用對偶格的原因將在下一段中變得清晰。因為誤差足夠短，輸入 v,e 由輸出 t 唯一定義，從 t 恢復它們正是 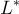上的一個平均情況 BDD 問題，可以假設（或證明）它是難解的。
或者，輸出可以是陪集 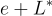的（規範公共代表），這消除了對（有些定義不明確的）「隨機」格向量 v 的需要。
使用 L 足夠短的陷門基底 S，可以使用標準格解碼演算法高效地反轉該函數，例如樸素取整或 Babai 最近平面演算法 [Bab85]。例如，取整演算法，給定 t=v+e，簡單地輸出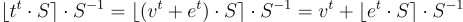

其中第二個等式成立是因為 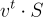是整數，因為 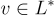。因此，只要對於每個短基底向量 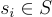都有 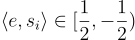。該演算法就能正確找到 v。只要 e 和 都足夠短，這確實成立，例如，根據 Cauchy-Schwarz 不等式，或依賴於 e 分佈的尾界。（最近平面演算法通常可以使用相同的基底從稍大的誤差中解碼，但計算效率較低。）

上述範本的 GPV 實例化（反轉該函數等價於搜尋-LWE 問題（回想一下，這是一個平均情況 BDD 問題））如下：

• 公鑰是一個均勻隨機的 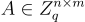指定格 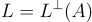連同 L 的一個相對短的陷門基底 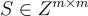生成，其中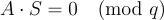

• 如第9章中所述，LWE 格 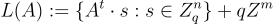是 L 的（縮放）對偶格，即 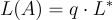。因此遵循上述範本，定義 LWE 函數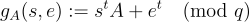
  
  其中應均勻隨機選擇輸入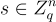

對應於「隨機」格向量 並從 LWE 誤差分佈 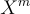中選擇 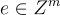。顯然，反轉此函數在語法上等價於搜尋-LWE n,q,χ,m 問題。

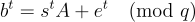• 使用陷門 S，可以從函數輸出 恢復 s,e，通過計算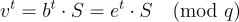
  

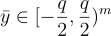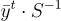將 y 提升為其規範代表 並輸出 ，其中 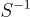，在有理數上計算，不模任何東西，作為 e 的期望值，從中也可以計算 s。請注意，只要 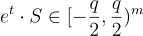不模任何東西，可以通過選擇相對於 e 和 的範數足夠大的 q 來確保這一點，那麼確實有 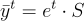，因此正確地恢復了 e。

離散高斯樣本:
在 GGH 簽章方案中，簽署消息大致對應於在平均情況下解決一個近似的最近向量問題(CVP)，這可以使用短基底來完成。與上述描述的基於單射 BDD 的函數相比，這裡目標可以是任意點，不需要特別接近格，並且它有許多對應於足夠接近的格向量的有效簽章。然而，回想一下，GGH 簽章方案及其一些衍生方案（例如[HHCP+03]）被證明是不安全的[NR06]，因為攻擊者可以使用少量簽章高效地重建秘密陷門基底。這是因為簽署演算法隱式地洩露了關於其使用的秘密基底幾何的資訊。

GPV 的工作給出了一種不同的、隨機化的簽署方法，該方法可證明不洩露關於秘密基底的任何資訊，除了其長度的界限，這已經是公開知識。一個關鍵屬性是，簽章的概率分佈是相同的，無論使用哪個短基底來產生它，因此簽章不會揭示任何關於陷門基底的資訊（除了它足夠短）。這一事實促進了在隨機預言模型中不可偽造性的形式化證明，假設類似 CVP 的問題（如 SIS）的平均情況難度。

GPV 方法背後的一個關鍵技術成分是給定任何足夠好的基底時，從離散高斯分佈中取樣的演算法。更精確地說，令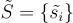
表示有序向量集 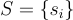的 Gram-Schmidt 正交化，並令 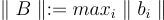對於任何向量集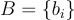

因此會有以下定理

定理 17.4.1.2 ([GPV08]):
存在一個隨機多項式時間演算法，給定格 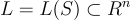的任何基底 S，任何陪集 c+L，以及任何高斯參數 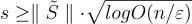輸出一個樣本，其分佈與離散高斯 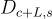的統計距離在 ε 以內。

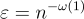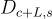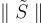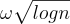通過將 ε 設置為例如 對於某個略超常數的函數 ω(1)，獲得了與 可忽略的統計距離，其參數 s 僅超過 一個小的 因子。

對於密碼學目的，定理 5.4.2 中的取樣演算法可以視為黑盒。然而，簡要提及，該演算法只是 Babai 的「最近平面」演算法 [Bab85] 的隨機化變體，在每次疊代中，在適當的陪集 c+Z 上的離散高斯分佈，而不是確定性的。後續的研究給出了其他取樣演算法，這些演算法在效率、統計誤差和取樣分佈的寬度之間提供了各種權衡，將在本小節末尾討論其中一些。

Klein [Kle00] 提出了基本相同的隨機化最近平面演算法變體，但用於一個非常不同的問題：有界距離解碼（BDD），且其參數 s 小於 Gram-Schmidt 向量的 最小 長度。對於此類參數，演算法的輸出分佈與離散高斯分佈相去甚遠。

原像可採樣函數 (Preimage Sampleable Functions — PSFs):
有了上述取樣演算法，可以描述 GPV 提出的 原像可採樣 陷門函數（PSFs）概念，這是一個通用的基於晶格的模板，以及一個基於 SIS 問題的具體實例化。從 PSFs 的半形式化定義開始。

定義 17.4.1.3 (原像可採樣函數):
一個可高效計算的函數 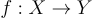其中定義域 X 賦予了某種可高效取樣的分佈 DD，如果存在一個高效的隨機演算法，記為 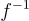使得以下兩種生成輸入-輸出對 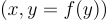的方法產生 相同的聯合分佈，在可忽略的統計誤差範圍內，則稱該函數是 原像可採樣 的：

• 正向 (Forward)：從輸入分佈中選擇 x←D，並令
  
• 反向 (Reverse)：從值域中均勻選擇 y←Y，然後取樣一個原像
  
  一個 PSF 族是此類函數的集合，可以高效地取樣（函數的描述）一個 f 連同其
  

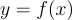
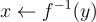
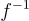
正如看到的，定義中的統計特性對於應用的安全性至關重要。注意到，任何陷門 雙射 族（例如，RSA 函數族）也是一個 PSF 族：原像「取樣」演算法實際上是確定性的，僅輸出唯一的原像。

上述定義不包含任何 安全性（或難度）標準，這些標準與取樣功能正交，因此應單獨考慮。可能要求的典型屬性包括 單向性 (one-wayness) 或 抗碰撞性 (collision resistance)。前者表示，給定一個取樣的 f 的描述，但不給 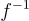和一個均勻隨機的 y←Y，要找到 y 在 f 下的 任何 原像是不可行的。後者表示，給定一個取樣的 f 的描述，要找到不同的輸入 x,x′ 使得 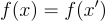是不可行的。

基於晶格的 PSFs:
現在描述 GPV 基於晶格的 PSFs 通用模板:

• 如上所述，函數 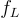的公開描述和陷門分別是晶格 的一個「困難」表示（例如，一個壞基底）和 L 的一個短基底 S。令 s 表示一個公開的高斯參數，該參數超過 L 的平滑參數，並且對 S 有適當的依賴關係，例如: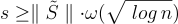
  

• 輸入分佈是 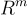上的（連續）高斯分佈 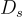在輸入 上評估 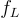僅僅輸出陪集 x+L 的（標準公開代表元），即 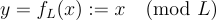強調，x 以壓倒性概率是相當 短 的，即 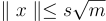但由於 L 的困難公開表示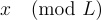， 幾乎總是由一個 長 向量表示。此外，因為 s 超過了 L 的平滑參數，輸出 y=x+L 在值域 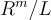上基本上是均勻的，符合要求。最後，為一個均勻陪集 y+L 找到一個有效的原像（即違反單向性）意味著在 y+L 中找到一個足夠短的向量，這本質上是一個平均情況下的近似 CVP 問題。

• 使用陷門基底 S 為給定陪集 y+L 取樣一個原像，只需從離散高斯分佈 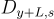中取樣，例如使用定理 17.4.1.2 中的演算法，該演算法要求 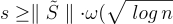稍微思考一下就會發現，因為原像的集合恰好是 y+L，並且每個 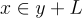在 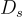下的條件概率與 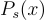成正比，所以 在條件限制為 獲得輸出 y+L 下的輸入分佈 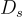恰好是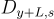

將這一點與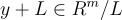

的（近似）均勻性結合起來，看到原像取樣演算法確實滿足了定義 5.4.3 中的統計特性。

上述模板的一個具體實例化如下，其單向性和抗碰撞性直接源於 SIS 問題的難度。它使用整數代替實數，因此使用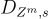
代替

• 如前所述，公鑰是一個均勻隨機的 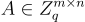指定了格(Lattice) 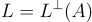，並同時生成一個相對較短的陷門基底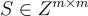

• 函數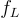
  就是 SIS 函數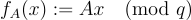
  
  這裡輸入 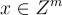，根據離散高斯分佈 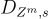選擇。從第8篇的回顧: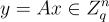
  

可以被視為陪集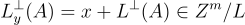

的標準代表元。因此，找到 y 的一個短原像在語法上等同於（非齊次）SIS 問題。類似地，一個有效的碰撞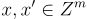
立即產生一個短的 SIS 解

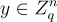• 要使用陷門基底 S 為 取樣一個原像，只需使用定理 17.4.1.2（或任何其他合適的演算法）中的演算法從離散高斯分佈 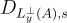中取樣。

擴展和隨機化短基底:
Cash, Hofheinz, Kiltz 和 Peikert [CHKP10] 展示了晶格陷門的其他有用特性，即它們可以被 擴展 (extended) 和 重新隨機化 (re-randomized)。這些特性被用於建構無需隨機預言機（random oracles）的數位簽章和基於身份的加密（IBE）方案，以及它們的 分層 (hierarchical) 版本，其中具有受限權限的私鑰可以安全地委派給下屬。

[CHKP10] 中的第一個主要思想是，對於奇偶校驗矩陣 A 的陷門短基底 S，可以為任意擴展 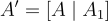其中 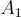是任意的，產生一個同等優質的陷門基底。具體來說，令 W 是 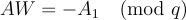的任何整數解，有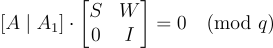

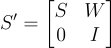
不難證明 S′ 確實是 的一個基底，並且其 Gram-Schmidt 向量 S′ 的長度不超過 S 的那些向量，因為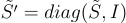

第二個主要思想是，對於 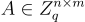的陷門基底 S 可以被重新隨機化為一個新的基底 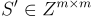該新基底不會洩露關於 S 的任何資訊（除了其品質的上限）。這只需使用 S 來取樣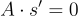
即 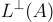中的晶格向量的獨立高斯解，直到累積了一組 m 個線性獨立的向量，然後可以將其轉換為一個基底。注意，結果基底 S′ 的品質大約比原始 S 差一個 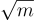因子，因為每個取樣解 s′ 的範數大約是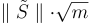

參考資料
[FO99a] E. Fujisaki and T. Okamoto. How to enhance the security of public-key encryption at minimum cost. In Public Key Cryptography, pages 53–68. 1999.

[FO99b] E. Fujisaki and T. Okamoto. Secure integration of asymmetric and symmetric encryption schemes. In CRYPTO, pages 537–554. 1999.

[BR93] M. Bellare and P. Rogaway. Random oracles are practical: A paradigm for designing efficient protocols. In ACM Conference on Computer and Communications Security, pages 62–73. 1993.

[Pei14] C. Peikert. Lattice cryptography for the Internet. In PQCrypto, pages 197–219. 2014.

[PW08] C. Peikert and B. Waters. Lossy trapdoor functions and their applications. SIAM J. Comput., 40(6):1803–1844, 2011. Preliminary version in STOC 2008.

[Pei09] C. Peikert. Public-key cryptosystems from the worst-case shortest vector problem. In STOC, pages 333–342. 2009.

[GPV08] C. Gentry, C. Peikert, and V. Vaikuntanathan. Trapdoors for hard lattices and new cryptographic constructions. In STOC, pages 197–206. 2008.

[MP12] D. Micciancio and C. Peikert. Trapdoors for lattices: Simpler, tighter, faster, smaller. In EUROCRYPT, pages 700–718. 2012.

[ABB10] S. Agrawal, D. Boneh, and X. Boyen. Efficient lattice (H)IBE in the standard model. In EUROCRYPT, pages 553–572. 2010.

[RSA78] R. L. Rivest, A. Shamir, and L. M. Adleman. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM, 21(2):120–126, 1978.

[Rab79] M. O. Rabin. Digitalized signatures and public-key functions as intractable as factorization. Technical Report MIT/LCS/TR-212, MIT Laboratory for Computer Science, 1979.

[Pai99] P. Paillier. Public-key cryptosystems based on composite degree residuosity classes. In EUROCRYPT ’99, pages 223–238. 1999.

[GGH97] O. Goldreich, S. Goldwasser, and S. Halevi. Public-key cryptosystems from lattice reduction problems. In CRYPTO, pages 112–131. 1997.

[CHKP10] D. Cash, D. Hofheinz, E. Kiltz, and C. Peikert. Bonsai trees, or how to delegate a lattice basis. J. Cryptology, 25(4):601–639, 2012. Preliminary version in Eurocrypt 2010.